513. 找树左下角的值 - 力扣(LeetCode)
思路:
- 迭代法:层序遍历二叉树,每次都将该层第一个值赋给
ans,最后返回ans - 递归法:前序遍历二叉树,遇到左右子树都为
nullptr则更新最大深度和结果值,每次递归进行前序遍历,即先递归左子树,再递归右子树,传递的深度值为depth + 1
我的AC代码
层序遍历迭代法
//时间复杂度O(n),空间复杂度O(n)
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
queue<TreeNode*> que;
int ans = root->val;
que.push(root);
while(!que.empty()) {
int qsize = que.size();
int qcnt = qsize;
while(qsize--) {
TreeNode* node = que.front();
if(qcnt - 1 == qsize) {
ans = node->val;
}
que.pop();
if(node->left) {
que.push(node->left);
}
if(node->right) {
que.push(node->right);
}
}
}
return ans;
}
};标准答案
递归(前序遍历)
//时间复杂度O(n),空间复杂度O(n)
class Solution {
public:
int maxDepth = INT_MIN;
int result;
void traversal(TreeNode* root, int depth) {
if (root->left == NULL && root->right == NULL) {
if (depth > maxDepth) {
maxDepth = depth;
result = root->val;
}
return;
}
if (root->left) {
depth++;
traversal(root->left, depth);
depth--; // 回溯
}
if (root->right) {
depth++;
traversal(root->right, depth);
depth--; // 回溯
}
return;
}
int findBottomLeftValue(TreeNode* root) {
traversal(root, 0);
return result;
}
};迭代(层序遍历)
//时间复杂度O(n),空间复杂度O(n)
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
int result = 0;
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
if (i == 0) result = node->val; // 记录最后一行第一个元素
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return result;
}
};112. 路径总和 - 力扣(LeetCode)
思路:递归法前序遍历二叉树,记录下所有的路径,每遇到一个节点就将节点值加上,如果遍历到的节点没有左右孩子则此时为路径末尾,判断总和是否与目标值相等,相等则将ans赋值为true
我的AC代码
//时间复杂度O(n),空间复杂度O(n)
//递归法(前序遍历)
class Solution {
public:
bool ans = false;
int target;
void findpath(TreeNode* node, int sum) {
if(!node->left && !node->right) {
sum += node->val;
if(sum == target) {
ans = true;
}
return;
}
sum += node->val;
if(node->left) {
findpath(node->left, sum);
}
if(node->right) {
findpath(node->right, sum);
}
}
bool hasPathSum(TreeNode* root, int targetSum) {
if(root == nullptr) {
return false;
}
target = targetSum;
int sum = 0;
findpath(root, sum);
return ans;
}
};标准答案
递归(前序遍历)完整版
//时间复杂度O(n),空间复杂度O(n)
class Solution {
private:
bool traversal(TreeNode* cur, int count) {
if (!cur->left && !cur->right && count == 0) return true; // 遇到叶子节点,并且计数为0
if (!cur->left && !cur->right) return false; // 遇到叶子节点直接返回
if (cur->left) { // 左
count -= cur->left->val; // 递归,处理节点;
if (traversal(cur->left, count)) return true;
count += cur->left->val; // 回溯,撤销处理结果
}
if (cur->right) { // 右
count -= cur->right->val; // 递归,处理节点;
if (traversal(cur->right, count)) return true;
count += cur->right->val; // 回溯,撤销处理结果
}
return false;
}
public:
bool hasPathSum(TreeNode* root, int sum) {
if (root == NULL) return false;
return traversal(root, sum - root->val);
}
};递归(前序遍历)精简版
//时间复杂度O(n),空间复杂度O(n)
class solution {
public:
bool hasPathSum(TreeNode* root, int sum) {
if (root == null) return false;
if (!root->left && !root->right && sum == root->val) {
return true;
}
return haspathsum(root->left, sum - root->val) || haspathsum(root->right, sum - root->val);
}
};迭代法(前序遍历)
//时间复杂度O(n),空间复杂度O(n)
class solution {
public:
bool haspathsum(TreeNode* root, int sum) {
if (root == null) return false;
// 此时栈里要放的是pair<节点指针,路径数值>
stack<pair<TreeNode*, int>> st;
st.push(pair<TreeNode*, int>(root, root->val));
while (!st.empty()) {
pair<TreeNode*, int> node = st.top();
st.pop();
// 如果该节点是叶子节点了,同时该节点的路径数值等于sum,那么就返回true
if (!node.first->left && !node.first->right && sum == node.second) return true;
// 右节点,压进去一个节点的时候,将该节点的路径数值也记录下来
if (node.first->right) {
st.push(pair<TreeNode*, int>(node.first->right, node.second + node.first->right->val));
}
// 左节点,压进去一个节点的时候,将该节点的路径数值也记录下来
if (node.first->left) {
st.push(pair<TreeNode*, int>(node.first->left, node.second + node.first->left->val));
}
}
return false;
}
};113. 路径总和 II - 力扣(LeetCode)
思路:递归法前序遍历二叉树,记录下所有的路径,每遇到一个节点就将节点值加上,如果遍历到的节点没有左右孩子则此时为路径末尾,判断总和是否与目标值相等,相等则将ans赋值为true并将路径添加到结果数组
我的AC代码
//时间复杂度O(n),空间复杂度O(n)
//递归法(前序遍历)
class Solution {
public:
int target;
void get_path(vector<vector<int>>& ans,int sum, vector<int>& path, TreeNode*node) {
sum += node->val;
path.push_back(node->val);
if(!node->left && !node->right) {
if(sum == target) {
ans.push_back(path);
}
}
if(node->left) {
get_path(ans, sum, path, node->left);
path.pop_back();
}
if(node->right) {
get_path(ans, sum, path, node->right);
path.pop_back();
}
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
vector<vector<int>> ans;
vector<int> path;
target = targetSum;
if(root == nullptr) {
return ans;
}
int sum = 0;
get_path(ans, sum, path, root);
return ans;
}
};标准答案
//时间复杂度O(n),空间复杂度O(n)
//递归法(前序遍历)
class solution {
private:
vector<vector<int>> result;
vector<int> path;
// 递归函数不需要返回值,因为我们要遍历整个树
void traversal(treenode* cur, int count) {
if (!cur->left && !cur->right && count == 0) { // 遇到了叶子节点且找到了和为sum的路径
result.push_back(path);
return;
}
if (!cur->left && !cur->right) return ; // 遇到叶子节点而没有找到合适的边,直接返回
if (cur->left) { // 左 (空节点不遍历)
path.push_back(cur->left->val);
count -= cur->left->val;
traversal(cur->left, count); // 递归
count += cur->left->val; // 回溯
path.pop_back(); // 回溯
}
if (cur->right) { // 右 (空节点不遍历)
path.push_back(cur->right->val);
count -= cur->right->val;
traversal(cur->right, count); // 递归
count += cur->right->val; // 回溯
path.pop_back(); // 回溯
}
return ;
}
public:
vector<vector<int>> pathsum(treenode* root, int sum) {
result.clear();
path.clear();
if (root == null) return result;
path.push_back(root->val); // 把根节点放进路径
traversal(root, sum - root->val);
return result;
}
};106. 从中序与后序遍历序列构造二叉树 - 力扣(LeetCode)
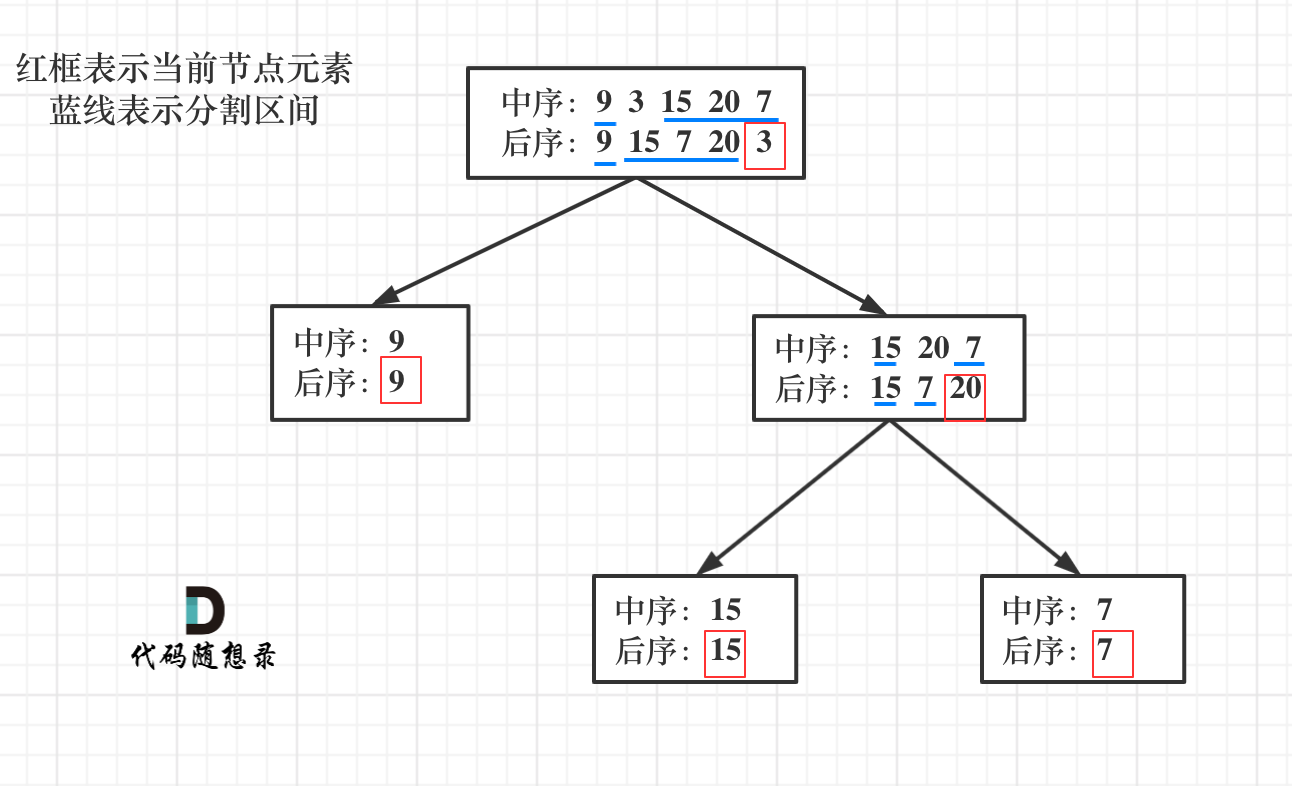
思路:想要用中序和后序遍历序列确定一个唯一的二叉树,就要每次以后序数组的最后一个元素为切割点,将中序数组分割成左右两份,再根据中序数组的分割情况来切割后序数组,如此反复,每次的切割点就是中间的节点
借用carl哥的图片帮助理解一下
我的AC代码
递归法(每次都定义新的vector)
//时间复杂度O(n),空间复杂度O(n2)
class Solution {
public:
TreeNode* build(vector<int>& inorder, vector<int>& postorder) {
int psize = postorder.size();
if(psize == 0) {
return nullptr;
}
TreeNode* root = new TreeNode(postorder[psize - 1]);
if(psize == 1) {
return root;
}
int sign = 0;
for(int i = 0; i < psize; ++i) {
if(inorder[i] == postorder[psize - 1]) {
sign = i;
break;
}
}
vector<int> leftinorder(inorder.begin(), inorder.begin() + sign);
vector<int> rightinorder(inorder.begin() + sign + 1, inorder.end());
postorder.resize(psize - 1);
vector<int> leftpostorder(postorder.begin(), postorder.begin() + leftinorder.size());
vector<int> rightpostorder(postorder.begin() + leftinorder.size(), postorder.end());
root->left = build(leftinorder, leftpostorder);
root->right = build(rightinorder, rightpostorder);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
int isize = inorder.size();
if(isize == 1) {
TreeNode* tmp = new TreeNode(inorder[0]);
return tmp;
}
return build(inorder, postorder);
}
};递归法(不重新定义新的vector而是建立索引,大大降低空间复杂度)
//时间复杂度O(n),空间复杂度O(n)
class Solution {
public:
TreeNode* build(vector<int>& inorder, int inbegin, int inend, vector<int>& postorder, int pobegin, int poend) {
int psize = poend - pobegin;
if(psize == 0) {
return nullptr;
}
TreeNode* root = new TreeNode(postorder[poend - 1]);
if(psize == 1) {
return root;
}
int sign;
for(int i = inbegin; i < inend; ++i) {
if(inorder[i] == postorder[poend - 1]) {
sign = i;
}
}
int leftinbegin = inbegin;
int leftinend = sign;
int rightinbegin = sign + 1;
int rightinend = inend;
int leftpobegin = pobegin;
int leftpoend = pobegin + sign - inbegin;
int rightpobegin = pobegin + sign - inbegin;
int rightpoend = poend - 1;
root->left = build(inorder, leftinbegin, leftinend, postorder, leftpobegin, leftpoend);
root->right = build(inorder, rightinbegin, rightinend, postorder, rightpobegin, rightpoend);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
int isize = inorder.size();
int psize = postorder.size();
return build(inorder, 0, isize, postorder, 0, psize);
}
};标准答案
递归法(每次都定义新的vector)
//时间复杂度O(n),空间复杂度O(n)
class Solution {
private:
TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
if (postorder.size() == 0) return NULL;
// 后序遍历数组最后一个元素,就是当前的中间节点
int rootValue = postorder[postorder.size() - 1];
TreeNode* root = new TreeNode(rootValue);
// 叶子节点
if (postorder.size() == 1) return root;
// 找到中序遍历的切割点
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// 切割中序数组
// 左闭右开区间:[0, delimiterIndex)
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
// [delimiterIndex + 1, end)
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
// postorder 舍弃末尾元素
postorder.resize(postorder.size() - 1);
// 切割后序数组
// 依然左闭右开,注意这里使用了左中序数组大小作为切割点
// [0, leftInorder.size)
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
// [leftInorder.size(), end)
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
root->left = traversal(leftInorder, leftPostorder);
root->right = traversal(rightInorder, rightPostorder);
return root;
}
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
return traversal(inorder, postorder);
}
};
递归法(不重新定义新的vector而是建立索引,大大降低空间复杂度)
//时间复杂度O(n),空间复杂度O(n)
class Solution {
private:
// 中序区间:[inorderBegin, inorderEnd),后序区间[postorderBegin, postorderEnd)
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& postorder, int postorderBegin, int postorderEnd) {
if (postorderBegin == postorderEnd) return NULL;
int rootValue = postorder[postorderEnd - 1];
TreeNode* root = new TreeNode(rootValue);
if (postorderEnd - postorderBegin == 1) return root;
int delimiterIndex;
for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// 切割中序数组
// 左中序区间,左闭右开[leftInorderBegin, leftInorderEnd)
int leftInorderBegin = inorderBegin;
int leftInorderEnd = delimiterIndex;
// 右中序区间,左闭右开[rightInorderBegin, rightInorderEnd)
int rightInorderBegin = delimiterIndex + 1;
int rightInorderEnd = inorderEnd;
// 切割后序数组
// 左后序区间,左闭右开[leftPostorderBegin, leftPostorderEnd)
int leftPostorderBegin = postorderBegin;
int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin; // 终止位置是 需要加上 中序区间的大小size
// 右后序区间,左闭右开[rightPostorderBegin, rightPostorderEnd)
int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);
int rightPostorderEnd = postorderEnd - 1; // 排除最后一个元素,已经作为节点了
root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, postorder, leftPostorderBegin, leftPostorderEnd);
root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);
return root;
}
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
// 左闭右开的原则
return traversal(inorder, 0, inorder.size(), postorder, 0, postorder.size());
}
};105. 从前序与中序遍历序列构造二叉树 - 力扣(LeetCode)
思路:与上一题一致,上一题的节点是后序遍历序列的最后一个,而这一题的节点是前序遍历序列的第一个
我的AC代码
// 时间复杂度O(n),空间复杂度O(n)
// 使用了建立下标索引的方法来优化空间复杂度
class Solution {
public:
TreeNode* build(vector<int>& preorder, int preBegin, int preEnd, vector<int>& inorder, int inBegin, int inEnd) {
int psize = preEnd - preBegin;
if(psize == 0) {
return nullptr;
}
TreeNode* root = new TreeNode(preorder[preBegin]);
if(psize == 1) {
return root;
}
int sign;
for(int i = inBegin; i < inEnd; ++i) {
if(inorder[i] == preorder[preBegin]) {
sign = i;
}
}
int leftInBegin = inBegin;
int leftInEnd = sign;
int rightInBegin = sign + 1;
int rightInEnd = inEnd;
int leftPreBegin = preBegin + 1;
int leftPreEnd = preBegin + sign - inBegin + 1;
int rightPreBegin = preBegin + sign - inBegin + 1;
int rightPreEnd = preEnd;
root->left = build(preorder, leftPreBegin, leftPreEnd, inorder, leftInBegin, leftInEnd);
root->right = build(preorder, rightPreBegin, rightPreEnd, inorder, rightInBegin, rightInEnd);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
return build(preorder, 0, preorder.size(), inorder, 0, inorder.size());
}
};标准答案
// 时间复杂度O(n),空间复杂度O(n)
// 使用了建立下标索引的方法来优化空间复杂度
class Solution {
private:
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& preorder, int preorderBegin, int preorderEnd) {
if (preorderBegin == preorderEnd) return NULL;
int rootValue = preorder[preorderBegin]; // 注意用preorderBegin 不要用0
TreeNode* root = new TreeNode(rootValue);
if (preorderEnd - preorderBegin == 1) return root;
int delimiterIndex;
for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// 切割中序数组
// 中序左区间,左闭右开[leftInorderBegin, leftInorderEnd)
int leftInorderBegin = inorderBegin;
int leftInorderEnd = delimiterIndex;
// 中序右区间,左闭右开[rightInorderBegin, rightInorderEnd)
int rightInorderBegin = delimiterIndex + 1;
int rightInorderEnd = inorderEnd;
// 切割前序数组
// 前序左区间,左闭右开[leftPreorderBegin, leftPreorderEnd)
int leftPreorderBegin = preorderBegin + 1;
int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin; // 终止位置是起始位置加上中序左区间的大小size
// 前序右区间, 左闭右开[rightPreorderBegin, rightPreorderEnd)
int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);
int rightPreorderEnd = preorderEnd;
root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, preorder, leftPreorderBegin, leftPreorderEnd);
root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);
return root;
}
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if (inorder.size() == 0 || preorder.size() == 0) return NULL;
// 参数坚持左闭右开的原则
return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());
}
};
Comments NOTHING