28. 找出字符串中第一个匹配项的下标 - 力扣(LeetCode)
思路:第一眼感觉快慢指针,所以命名用了fast,请大佬忽略呜呜呜,后来我发现只是有点类似快慢指针。遍历数组,遇到和needle开头一样的字母就逐个进行比对,如果全部一致,则返回答案,如果有一个不同,立即结束,每次不管有没有找到,都执行fast++,如果全部跑完也没有,就return -1
正规的思路应该是KMP,我这边属于是野路子暴力算法直接给过了,但是不知道为啥时间也是0ms,可能leetcode的样例比较弱,这边介绍一下KMP写法
- 先构造
next数组,即前缀表,用来回退 - 接着遍历文本串,如果遇到不符合的就回退
j(j代表的是前缀长度)到相应的位置,符合就执行j++,如果此时j的值已经达到字符串的长度,那么说明全部验证完毕,则返回答案,如果遍历完成以后还是没有找到符合条件的字符串,则返回-1
具体的KMP代码讲解请看代码随想录 以LeetCode题28.strStr(),为切入点详解KMP,里面讲得很生动形象,还有相关的动图和视频可以辅助理解
我的AC代码
//时间复杂度O(n2),空间复杂度O(1)
class Solution {
public:
int strStr(string haystack, string needle) {
int hsize = haystack.size();
int nsize = needle.size();
int fast = 0;
while(fast < hsize) {
if(haystack[fast] == needle[0]) {
if(nsize == 1) {
return fast;
}
for(int i = fast + 1; i < nsize + fast ; ++i) {
if(needle[i - fast] != haystack[i]) {
break;
}
else {
if(i == nsize + fast - 1) {
return fast;
}
}
}
}
fast++;
}
return -1;
}
};标准答案
写法一: KMP前缀表统一减一实现
//时间复杂度O(n + m),空间复杂度O(m)
class Solution {
public:
void get_next(int* next, const string& s) {
int j = -1;
next[0] = j;
int scnt = s.size();
for(int i = 1; i < scnt; ++i) {
while(j > -1 && s[j + 1] != s[i]) {
j = next[j];
}
if(s[j + 1] == s[i]) {
++j;
}
next[i] = j;
}
}
int strStr(string haystack, string needle) {
int hcnt = haystack.size();
int ncnt = needle.size();
if(ncnt > hcnt) {
return -1;
}
int next[ncnt];
get_next(next, needle);
for(int i = 0;i < ncnt; ++i) {
cout << next[i];
}
int j = -1;
for(int i = 0;i < haystack.size(); ++i) {
while(j > -1 && needle[j + 1] != haystack[i]) {
j = next[j];
}
if(needle[j + 1] == haystack[i]) {
j++;
if(j == ncnt - 1) {
return i - ncnt + 1;
}
}
}
return -1;
}
};写法二: KMP前缀表不减一实现
//时间复杂度O(n + m),空间复杂度O(m)
class Solution {
public:
void getNext(int* next, const string& s) {
int j = 0;
next[0] = 0;
for(int i = 1; i < s.size(); i++) {
while (j > 0 && s[i] != s[j]) {
j = next[j - 1];
}
if (s[i] == s[j]) {
j++;
}
next[i] = j;
}
}
int strStr(string haystack, string needle) {
if (needle.size() == 0) {
return 0;
}
int next[needle.size()];
getNext(next, needle);
int j = 0;
for (int i = 0; i < haystack.size(); i++) {
while(j > 0 && haystack[i] != needle[j]) {
j = next[j - 1];
}
if (haystack[i] == needle[j]) {
j++;
}
if (j == needle.size() ) {
return (i - needle.size() + 1);
}
}
return -1;
}
};其实减不减一无所谓,本质上都是一样的,只是代码实现上有细微的差别,选择顺手的即可
459. 重复的子字符串 - 力扣(LeetCode)
思路:刚开始看错题目了,以为是字符串中有重复子串,打算直接用map记录所有相邻两个字母的组合,如果出现重复的直接返回true,后来发现有些样例过不了,重新看了眼题目,才发现是字符串由重复的子串构成,那么就直接用KMP。只要是由重复的子字符串构成的,next前缀表最后的那个数字一定大于-1,而且最小子串多次重复后可以构成该字符串。有了这个思路题目就好写了。但我这里的解法有点反人类,先构造next表,然后间隔每最大子串的长度进行循环,看看每个间隔与最大子串是否完全相同,即检查这个字符串是否由最大子串构成,这个检查虽然无法完全跑完,但是因为重复子串非常神奇,如果有多段,这几段都会是一样的,所以最后还是能照常完成检验,如果是则返回true,否则返回false
其实这题还有更暴力的写法,直接找前后两段相同的最大子串,然后按上面的思路开始遍历就行了
正规的写法还是看代码随想录|重复的子字符串,极其详尽!
我的AC代码
//时间复杂度O(n + m),空间复杂度O(m)
class Solution {
public:
void get_next(int* next ,const string& s) {
int j = -1;
next[0] = -1;
int scnt = s.size();
for(int i = 1; i < scnt; ++i) {
while(j > -1 && s[j+1] != s[i]) {
j = next[j];
}
if(s[j + 1] == s[i]) {
++j;
}
next[i] = j;
}
}
bool repeatedSubstringPattern(string s) {
int scnt = s.size();
int next[scnt];
get_next(next, s);
int mmax = next[scnt - 1] + 1;
if(mmax == 0) {
return false;
}
for(int i = 0; i < scnt; i += mmax) {
for(int j = i; j < i + mmax; ++j) {
if(s[j] != s[j - i]) {
return false;
}
if(j == scnt - 1 && s[j] == s[j - i]) {
return true;
}
}
}
return false;
}
};标准答案
天才的想法(拼接字符串)
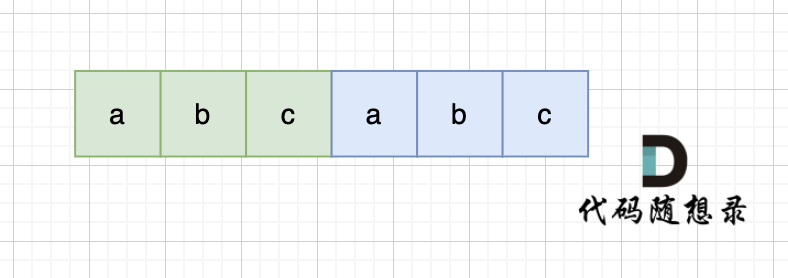
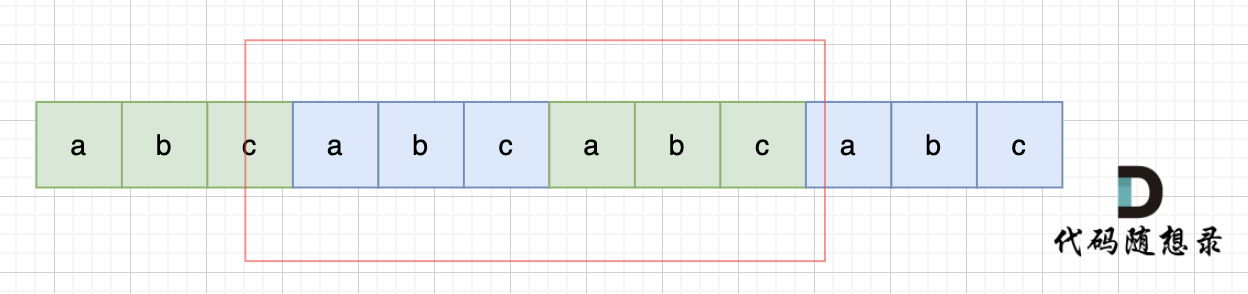
当一个字符串s内部有重复的子串组成,那么这个字符串一定是前后都由相同的子串组成。那么既然前面有相同的子串,后面有相同的子串,那么把两个字符串s拼接起来,在这样组成的字符串中,后面的子串做前串,前后的子串做后串,就一定还能组成一个s,所以判断字符串s是否有重复子串组成,只要两个s拼接在一起,里面还出现一个s的话,就说明是又重复子串组成。
当然,我们在判断 s + s 拼接的字符串里是否出现一个s的的时候,要刨除 s + s 的首字符和尾字符,这样避免在s+s中搜索出原来的s,我们要搜索的是中间拼接出来的s。(引用自代码随想录)
//时间复杂度O(n + m),空间复杂度O(m)
class Solution {
public:
bool repeatedSubstringPattern(string s) {
string t = s + s;
t.erase(t.begin()); t.erase(t.end() - 1); // 掐头去尾
if (t.find(s) != std::string::npos) return true; // r
return false;
}
};KMP
//时间复杂度O(n + m),空间复杂度O(m)
class Solution {
public:
void getNext (int* next, const string& s){
next[0] = -1;
int j = -1;
for(int i = 1;i < s.size(); i++){
while(j >= 0 && s[i] != s[j + 1]) {
j = next[j];
}
if(s[i] == s[j + 1]) {
j++;
}
next[i] = j;
}
}
bool repeatedSubstringPattern (string s) {
if (s.size() == 0) {
return false;
}
int next[s.size()];
getNext(next, s);
int len = s.size();
if (next[len - 1] != -1 && len % (len - (next[len - 1] + 1)) == 0) {
return true;
}
return false;
}
};
Comments NOTHING